I teoremi sono il peggior incubo di chi odia la matematica e la fisica. Questo perché sono spesso considerati troppo teorici e avulsi dalla realtà, con il loro lessico specifico e il modo articolato di porre i concetti. Oggi vogliamo rivalutarli, dedicando un intero articolo ad un teorema, non solo essenziale per studiare l’affascinante mondo della fluidodinamica, ma anche legato alla storia della casata reale inglese. Ladies and gentlemen, ecco a voi il teorema di Buckingham.
Le origini di Buckingham
Tutto ha inizio nel Buckinghamshire, una deliziosa contea alle porte di Londra. Come spesso accadeva nel passato, il cognome della famiglia che la governava arrivava dalla regione stessa: Buckingham. Uno di questi duchi costruì un’umile dimora nel cuore di Londra, oggi nota come Buckingham Palace, la casa dei reali inglesi. Un altro ramo della famiglia invece andò a cercare fortuna nel nuovo mondo, salpando verso Boston. Tra gli eredi di questi avventurieri figura Edgar Buckingham, un matematico americano che formulò un teorema così importante da essere associato al suo cognome: il teorema di Buckingham.


Figura 1: a sinistra una veduta campestre della contea del Buckinghamshire, a destra un ritratto di Edgar Buckingham (fonti: Alltrails e Carnotcycle)
Dalle campagne ai numeri adimensionali
Una storia così interessante non può che presagire un teorema altrettanto interessate. Ed è proprio così: grazie ad esso si riescono a semplificare equazioni con tante variabili, ottenendone delle altre molto più semplici da gestire. L’enunciato è il seguente:
| “data un’equazione dimensionalmente omogenea funzione di K grandezze fisiche, essa può essere ridotta a un’altra equazione dipendente da (K-P) numeri adimensionali, dove P è il numero di grandezze fondamentali del sistema di unità di misura” |
\[ f ( x_{1} , x_{2} , … , x_{k} ) = g ( y_{1} , y_{2} , … , y_{k – p} ) \]
Traduciamo facendo un esempio nel campo della fluidodinamica, la branca della scienza che studia l’incantevole comportamento dei fluidi. Immaginiamo di dover studiare un liquido che scorre in un condotto. Le grandezze fisiche K sono in questo caso la sua velocità, la dimensione del condotto e le proprietà del fluido (densità, calore specifico, viscosità, trasmittanza termica, coefficiente di scambio termico convettivo): il totale ammonta a 7. Le grandezze fondamentali P sono quelle definibili in maniera universale, dalle cui unità di misura dipendono tutte le altre. Un modo molto complicato per indicare il tempo, la lunghezza, la massa e la temperatura: siamo a 4. Calcolatrice alla mano: K-P = 7-4 = 3.
Il teorema spiegato facile
Il teorema dice che invece di risolvere un’equazione complicatissima con 7 variabili possiamo risolverne un’altra molto più semplice, perché funzione solo di 3 numeri adimensionali. Ma che cosa sono questi strani numeri? Sono un insieme di grandezze raggruppate in modo tale che le loro unità di misura si annullino tra loro, risultando in una quantità per l’appunto adimensionale. Vi ricordate quando al liceo vi dimenticavate di mettere le unità di misura e la prof strillava: “Che cosa sono queste? Mele? Pere?”. In questo caso avreste ragione voi.
I numeri adimensionali sono fondamentali in questo campo della scienza, perché ci permettono di comprendere con chiarezza i comportamenti dei fluidi. Ecco quindi che insiemi di grandezze apparentemente casuali sono invece densi di significato, proprio grazie al teorema di Buckingham. Lunga vita al re Edgar.
Numero di Reynolds
Parliamo nel dettaglio di ciascuno di questi tre numeri in grado di farci risolvere i complessi problemi di fluidodinamica. Partiamo forse dal più importante: il numero di Reynolds. È composto in questo modo:
\[ Re = \frac{ \rho \nu D } { \mu } \]
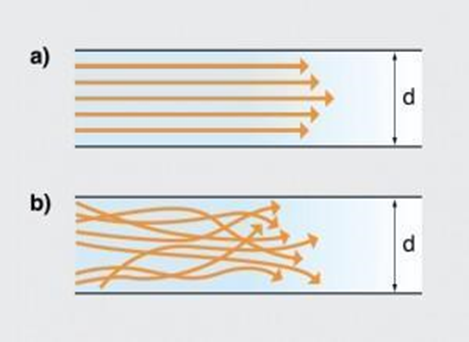
dove \[ \rho \] è la densità del fluido, \[ \nu \] la sua velocità, \[ D \] il diametro del condotto e \[ \mu \] la viscosità (avete presente la lentezza del miele a cadere dal cucchiaino? Deriva dalla sua viscosità molto alta). Il numero di Reynolds sta a significare il rapporto tra le forze d’inerzia, quelle che spingono il fluido a muoversi, e le forze viscose, quelle che lo frenano a causa degli attriti. Quando si studia il deflusso in un condotto la prima cosa da fare è calcolare il valore di questo numero, poiché indica il regime del moto, cioè in che modo il fluido si muove. Con valori bassi, \[ Re < 2300 \], si ha un regime laminare: tutte le molecole scorrono parallelamente le une alle altre senza scontrarsi mai, come le macchine in un’autostrada dalle infinite corsie. Con valori alti, \[ Re > 4000 \], si ha un regime turbolento: il regno del caos. Le particelle si scontrano e si deviano a vicenda, formando turbinanti vortici come nella Notte stellata di Van Gogh. E in mezzo? Tra 2300 e 4000 si ha la zona di transizione, un modo elegante per dire che non si ha la più pallida idea di che cosa stia succedendo… Insomma, un semplice numero è in grado di darci tante informazioni sul moto dei fluidi, e siamo solo all’inizio!
Numero di Prandtl
Il secondo protagonista è il numero di Prandtl, così composto:
\[ Pr = \frac{ \mu c_{p} } { \lambda } \]
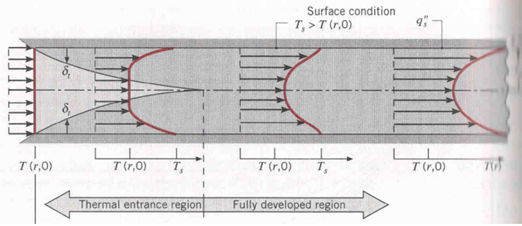
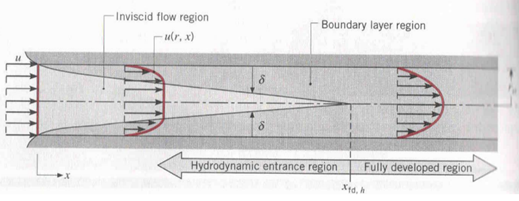
Dove \[ \mu \] è la viscosità, \[ c_{p} \] la capacità termica (quanto un corpo aumenta di temperatura se scaldato) e \[ \lambda \] la trasmittanza termica (quanto un corpo è bravo a condurre il calore: se lasciate un cucchiaio di metallo nella pentola sul fuoco e lo toccate vi brucerete, perché al contrario dei mestoli in legno i metalli hanno una molto alta). Questo numero ci racconta lo sviluppo del fluido all’interno del condotto. All’ingresso del tubo, tutto il liquido è alla stessa velocità e temperatura. Ma andando avanti, la parte di fluido a contatto con la parete rallenterà, a causa degli attriti, e cambierà di temperatura, perché a contatto con una superficie a temperatura differente. Ci vuole quindi un certo spazio prima che i profili di velocità e di temperatura si consolidino, cioè rimangano invariati con l’andare avanti nel condotto. Questo spazio si chiama regione di ingresso e ce ne sono due: una fluidodinamica, legata alla velocità, e una termica, legata alla temperatura. Il numero di Prandtl è il loro rapporto. Se è piccolo vuol dire che il calore diffonderà molto velocemente, mentre le velocità si assesteranno in un secondo momento: è il caso dei metalli liquidi. Se invece il numero è grande il fluido si svilupperà prima dal punto di vista della velocità e solo dopo in temperatura, come capita agli oli. D’ora in poi se volete stupire i vostri amici a cena potete fare i sofisticati dicendo: “Quest’olio è molto buono, ha un alto numero di Prandtl”.
Numero di Nusselt
Arriviamo all’ultimo numero, ma non per importanza: il numero di Nusselt.
\[ Nu = \frac{ h D } { \lambda } \]
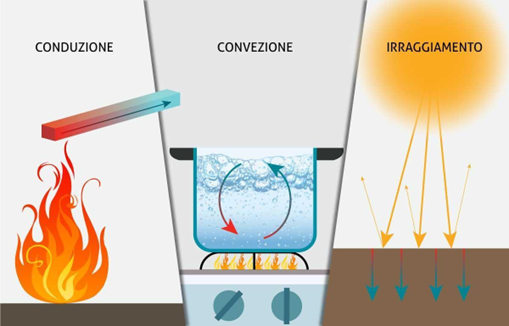
Dove \[ h \] è il coefficiente di scambio termico convettivo (che vi spieghiamo tra pochissimo), \[ D \] il diametro del condotto e \[ \lambda \] la trasmittanza termica. Questo numero mette a confronto le due modalità principali con cui un fluido può scambiare calore: la conduzione e la convezione (in realtà ne esiste anche una terza, l’irraggiamento, ma essendo completamente diverso dagli altri due, perché veicolato da onde elettromagnetiche, non può essere messo a confronto). La conduzione del calore è quel meccanismo di scambio termico per contatto. Vi è mai capitato di toccare una pentola bollente bruciandovi? Colpa della conduzione. La convezione invece è il meccanismo di scambio di calore causato dal movimento dei fluidi. Avete presente quando d’estate un bel venticello fresco vi dona refrigerio? Ringraziate la convezione.
Il coefficiente di scambio termico convettivo \[ h \] racchiude in sé tutte le caratteristiche della convezione del calore. È così ricco e completo da essere impossibile da calcolare con una formula semplice! Ecco quindi che torna in nostro soccorso il teorema di Buckingham. Grazie ad esso possiamo scrivere una formula che leghi i tre numeri di cui abbiamo parlato oggi: Reynolds, Prandtl e Nusselt. I primi due sono facilmente calcolabili e ci permettono di ottenere Nusselt, da cui si ricava . Soltanto in questo modo siamo in grado di studiare i fenomeni legati alla convezione del calore nei fluidi.
Tiriamo le somme
Eccoci alla fine del nostro lungo viaggio. Siamo partiti dall’Inghilterra, per poi emigrare in America per conoscere Edgar Buckingham, l’uomo che con il suo teorema ha spalancato le porte del regno dei numeri adimensionali. Grazie a questi insiemi di grandezze siamo in grado di descrivere il comportamento dei fluidi, con il quale possiamo comprendere il mondo che ci circonda, meravigliandoci con esso. È proprio il caso di dirlo: quando si parla di numeri adimensionali, l’insieme è più grande della somma delle singole parti.
Abbiamo stimolato la tua curiosità? Puoi saperne di più consultando le nostre fonti:



Lascia un commento